빛은 입자이며, 빛의 경로는 열린 가능성이다 - 파인만 -

일반인을 위한 파인만의 QED 강의
리처드 파인만 지음, 박병철 옮김 / 승산 / 2001년 8월

'빛과 물질의 상호작용을 양자역학적으로 설명하는 이론이 일단의 물리학자들에 의해 1929년 빛을 보게 되었으며, 거기에는 "양자전기역학"이라는 끔찍한 이름이 붙여졌다.'(p27)

<일반인을 위한 파인만의 QED 강의>는 제목 그대로 양자전기역학(QED ; Quantum Electrodynamics)을 일반인들이 이해하기 쉽게 설명한 책이다. 파인만(Richard P. Feynman, 1918 ~ 1988) 은 어려운 수학 대신 이 책에서는 기초적인 확률법칙과 '화살표'를 이용하여 어려운 개념을 설명하고 있다.

그렇다면, 이 책 <일반인을 위한 파인만의 QED 강의>에서 설명하고자 하는 개념은 무엇일까? 전체 4강(講)으로 구성된 본문에서 이 개념을 설명하고 있다. 

'폴 디랙 Paul Dirac은 그의 이론을 통하여 전자가 자기능률 magnetic moment(작은 자석에 의한 힘과 비슷한 개념)을 갖고 있으며 그 세기는 특정한 단위를 썼을 때 정확하게 1이 되어야한다고 주장하였다... 줄리안 슈위거 Julian.S. Schwinger는 "야바위 놀음 shell-game"을 사용하여 처음으로 올바른 자기능률값을 계산해냈다. 그 결과는 1.0116이었는데 이것은 실험치와 매우 비슷한 값이었으므로 우리의 계산법이 옳다는 사실을 입증한 셈이었다. 내가 여러분에게 앞으로 설명하게 될 이론이 바로 이것이다.'(p29)

1. 빛은 입자다 

 파인만이 설명하는 '빛 Light'은 눈에 보이는 빛만을 의미하지 않는다. 우리는 일반적으로 빛이 파동운동을 하는 것으로 알고 있는데 이러한 고정관념을 버릴 것을 파인만은 요청한다.

'내가 말하는 빛이란, 적색에서 파란색에 걸쳐 있는 가시광선만을 뜻하는 게 아니다. 가시광선은 빛의 일부분에 지나지 않는다... 자외선, 적오선, TV파, 라디오파등으로 옮겨간다. 이 모든 것들이 다 "빛"이다...눈에 보이는 것만이 실재라면 물리학은 당장 와해된다.'(p39)

'나는 빛이 입자처럼 행동한다는 점을 여러분에게 강조하는 바이다. 이것을 머리속에 새겨두기 바란다. 특히 학교에서 "빛은 파동처럼 행동한다."고 배웠던 사람들에게 강조한다. 다시 한 번 말하건대 빛은 정말로 입자처럼 행동하고 있다.'(p41)

2. 빛은 어떤 경로로 움직이는가?

[그림2] p43

전등에서 나온 빛이 유리판에서 반사되어 일부가 감지기에 도달하는 실험을 통해 파인만은 부분반사의 개념에 대해 의문을 제기한다. 특히 이러한 부분 반사 현상은 유리판 양면(윗면과 아랫면)에서 이러한 현상을 관찰했을 때 더 극명하게 발견하게 된다.

 가. 부분반사

'실험 결과, 광원에서 곧장 90도 아래 유리판으로 향한 100개의 광자 중에서 평균적으로 4개가 A에 도달하고 96개는 유리표면을 통과하여 B에 도달한다는 사실이 알려졌다. 즉, 이경우에 4%의 광자만이 반사되고 나머지 96%는 유리를 투과한다는 것을 뜻한다. 어떻게 입사된 빛의 일부만이 반사된다는 말인가? 개개의 광자는 A로 갈 수도 있고 B로 갈 수도 있다. 광자는 자신의 갈 길을 어떻게 결정하는가?'(p44)

[그림4] p47

빛의 부분반사 문제를 해결하기 위해 파인만은 '화살표'를 활용한다. 본문에서 화살표의 길이와 방향은 확률의 크기와 빛의 방향성을 의미한다. 

[그림6] 유리판의 양면에서 일어나는 부분반사현상을 설명하려면, 하나의 사건이 일어날 확률만을 알아내는데 만족해야 한다. 그리고 이 확률은 양자전기역학을 이용하여 계산할 수 있다. 화살표 하나를 그려서, 그로부터 만들어지는 정사각형의 면적이 곧 확률이 된다.(p53)

'어떤 특정한 사건이 일어날 확률과 화살표 사이에는 어떤 관계가 있는가? 사건이 일어날 확률은 화살표의 길이의 제곱과 같다.'(p52)

화살표의 합성 법칙은 다음과 같이 '기본법칙'과 '일반법칙'으로 구분할 수 있다.

'1) 기본법칙 : 하나의 사건이 일어날 확률은 "확률진폭 Probability amplitude"이라 불리는 화살표의 길이의 제곱과 같다. 예를 들어 길이가 0.4인 화살표는 0.16 또는 16%의 확률을 나타낸다.

2) 일반법칙 : 하나의 사건이 일어날 수 있는 방법이 여러 가지 있을 때에는 각각에 대해 화살표를 그린 후 화살표의 머리를 다른 화살표의 꼬리에 갖다 붙임으로써 이들을 합성(덧셈)하여 최종 화살표(첫번째 화살표 꼬리에서 마지막 화살표 머리를 이어준 화살표)를 그린다.(갖다 붙이는 순서에는 무관하다.) 이렇게 만들어진 최종 화살표의 길이를 제곱한 값이 곧 사건이 일어날 전체 확률을 나타낸다.'(p71)

'어느 특정한 사건이 일어날 확률은 합성된 최종 화살표 길이의 제곱과 같다. 그리고 최종 화살표는 그 사건이 일어날 수 있는 모든 가능한 경우의 화살표들을 합성하여(또는 더하여) 얻어진다.'(p74)

 <일반인을 위한 파인만의 QED 강의>에 있어 가장 중요한 내용은 [그림24]로 생각된다. 이 내용을 기초로 하여 파인만은 빛의 이중성, 빛의 산란, 빛의 투과 현상을 설명하는데, 중요한 내용은 다음 그림에서 대부분 설명된다.

[그림24] 빛이 거울에서 반사되어 감지기에 도달하는 모든 가능한 경로들이 그림의 상단부에표시되어 있다. 중앙부의 그림은 각 경로에 소요되는 시간을 세로축에 표시한 그래프이다. 그래프 아래에 그려진 화살표는 각 경로에 해당되는 화살표의 방향을 나타내며, 가장 하단에는 이 모든 화살표들을 합성한 최종 화살표가 굵은 선으로 표시되어 있다. 최종 화살표의 길이는 주로 E에서 I 사이의 화살표에 의해 생긴다. 왜냐하면 그 사이에 있는 경로들은 길이가 서로 비슷하여 화살표의 방향도 서로 엇비슷하기 때문이다. 그리고 이 지점은 소요시간이 가장 적은 편에 속하는 경로들이 밀집되어 있는 지역이므로, 빛이 최단 시간 경로를 따라서 진행한다고 말해도 크게 틀리지 않는다.(p78)

 [그림24]를 통해서 파인만은 빛이 입자처럼 운동하고 있으며, 빛은 무한히 많은 경로를 통해 운동하고 있으나. 확률에 따라 실제 우리에게 관측되는 빛의 운동은 최단경로를 따라 진행된다는 것을 설명하고 있다.

결국 <일반인을 위한 파인만의 QED 강의>에서 파인만은 '빛이 한 점에서 다른 점으로 가는데 직진만 하는 것이 아니라 가능한 모든 길을 동시에 지나간다'는 사실을 기초로 하여 '전자 자체는 희미하게 퍼져 있는 안개같은 존재이나 빛으로 관측할 때는 뚜렷한 점으로 보인다'는 사실을 우리에게 설명하고 있다.  

 본 리뷰에서 직접 다루지 않았지만, 간섭현상등을 설명하는 3장, 4장에서는 확률의 덧셈법칙과 곱셈법칙을 이용하여 내용을 설명하고 있다. 책에서 활용되는 확률의 두 법칙은 아래와 같다. 

[확률의 두 가지 합성법칙 rule of composition]

'1) 덧셈법칙 : 한 사건이 여러 가지의 독립적 경로를 통하여 발생 가능한 경우에는 각 경로를 지나갈 확률을 모두 더한다.

2) 곱셈법칙 : 한 사건이 순차적인 여러 단계를 거쳐 발생하는 경우에는 각 단계의 확률을 모두 곱한다.'(p128)

<일반인을 위한 파인만의 QED강의>는 최소한의 수학(확률의 법칙)과 화살표를 활용하여 양자전기역학(QED)의 핵심(核心)을 잘 설명하고 있다. 그럼에도 양자물리학의 세계가 워낙 어렵기 때문에, 우리와 같은 일반인들이 이해하기는 쉽지 않은 것도 사실이다. 이 책의 모든 내용을 이해하기위해 노력하기보다 양자물리학의 세계가 확정성의 세계가 아닌 '불확정성의 세계'라는 것을 이해하고, '열린 가능성'을 우리가 진정으로 깨달을 수 있다면 그것으로 이 책의 목적은 달성한 것이 아닐까하는 생각을 해본다.

몰랐어? 문제는 선거제도야

 

<몰랐어? 문제는 선거제도야>는 비례 민주주의 연대에서 발행한 소책자이며, 다소 생소할 수 있는 '연동형 비례대표제'를 담고 있다. 이 책자의 핵심 내용인 연동형 비례대표제는 정당이 얻은 득표율과 국회의석비율을 일치시키는 것을 의미한다.(p11) 이번 제19대 대통령 선거결과를 보면서 우리나라의 다수결 투표제에 대해 다시 생각하면서, 책에서 소개한 연동형 비례 대표제 이외에 추가적으로 적용되었으면 하는 제도 개선안을 몇 가지 정리해 본다.

1. 연동형 비례 대표제

'연동형 비례대표제는 정당이 얻은 득표율에 따라 전체 국회의석을 배분하는 제도이다. 예를 들어 국회의 총의석이 100석, 지역구가 50 있다고 가정해보자. 이 때 A정당은 "정당 투표"로 얻은 득표율이 30%, 지역구 20명 당선이라면, A정당은 일단 총의석 100개의 3%인 30석을 확보한다. 그 중 20석은 지역구 의원에게 돌아가고 나머지 10석은 A정당의 비례대표후보들이 채우게 된다.'(p16)

[그림] 연동형 비례 대표제

소책자에서는 '연동형 비례대표제'의 장점은 '공정하다', '다양한 목소리가 국회에 들어갈 수 있다', '정책의 질(質)이 좋아진다', '지역구도가 자연스럽게 완화된다' 등을 제시한다. 책에서 제안한 연동형 비례 대표제 이외에 추가적인 제도 개선안을 살펴보자. 

2. 다수결 투표의 대안 : 승인 투표 

 승자독식(勝者獨食)의 현재 투표제를 보완할 수 있는 방안 중 하나가 '승인 투표'제다. 승인 투표제는 일종의 누적투표법이다. 이를 통해 유권자는 자신의 선호에 대해 분명하게 표시할 수 있다. (관련 내용 : http://blog.aladin.co.kr/702641187/9281752)

'예를 들어, "승인투표(approval voting)"는 각 투표자가 후보마다 하나의 표를 던지는 제도이다. "투표자 한 사람이 한 표"에서 "한 후보에 한 투표"로 바꾸는 것이다. 그런 식으로 하면, 한 명의 투표자가 자신이 좋아하는 후보자에게 모두 "승인하는" 표를 던질 수 있다.... 파울루스가 훨씬 좋아하는 제도는 누적투표법(accumulative voting)이다. 이 제도에서 투표자는 자신이 강렬한 지지를 보내는 후보자(또는 쟁점)에게 여러 표를 누적해서 던질 수 있다. 이 제도 에서는 투표자가 가장 중요한 논점에 초점을 두는 것이 가능하다.'<아름다운, 너무나 아름다운 수학> (p131)

 아직 일반선거에는 승인 투표가 인정받고 있지 못하지만, 상법(商法)에는 이미 소수주주의 권익을 보호하는 집중투표제도를 상법 제382조의 내용으로 인정하고 있다. 다만, 회사 정관에서 이를 배제하는 경우에는 행하지 못하기 때문에 이를 시행하고 회사 수는 매우 적다. 향후 경제 민주화가 진행된다면, 이에 대한 제도적 개선과 확대시행이 되지 않을까 생각해본다.  집중투표제가 보다 널리 사회적으로 받아들여진다면, 선거권의 변화도 생각해 볼 수 있지 않을까.

'집중투표제도(集中投票制, cumulative voting)는 이사를 선임함에 있어서 선임하고자 하는 이사의 수만큼의 의결권을 1주식의 주주에게 부여하는 제도이다. 이는 1주 1의결권의 원칙에 대한 예외이며 소수파 주주도 자기가 적당하다고 생각하는 사람을 이사로서 선임하여 이사회에 진출시킬 수 있도록 한 제도이다. 이 제도에 따르면 2명 이상의 이사 선임을 목적으로 열리는 주주총회에서 주주는 1주마다 선임예정 이사와 같은 수의 의결권을 가지며(의결권=보유주식 수×이사후보수) 이 의결권을 후보자 한 사람 또는 몇 명에게 집중적으로 행사하여 득표 수에 따라 차례로 이사를 선임하게 된다.' (출처 : 위키피디아)

'대한민국 상법 제382조의2(집중투표) ① 2인 이상의 이사의 선임을 목적으로 하는 총회의 소집이 있는 때에는 의결권없는 주식을 제외한 발행주식총수의 100분의 3 이상에 해당하는 주식을 가진 주주는 정관에서 달리 정하는 경우를 제외하고는 회사에 대하여 집중투표의 방법으로 이사를 선임할 것을 청구할 수 있다.

③제1항의 청구가 있는 경우에 이사의 선임결의에 관하여 각 주주는 1주마다 선임할 이사의 수와 동일한 수의 의결권을 가지며, 그 의결권은 이사 후보자 1인 또는 수인에게 집중하여 투표하는 방법으로 행사할 수 있다.

④제3항의 규정에 의한 투표의 방법으로 이사를 선임하는 경우에는 투표의 최다수를 얻은 자부터 순차적으로 이사에 선임되는 것으로 한다.'

3. 전체 국민에게 1표를

 저출산 고령화 시대에 전체 선거인구 중 노령인구의 비중이 늘어가면서 일부에서 노인 선거권 제한에 대한 이야기도 나오고 있는 것은 사실이다. 그렇지만, 국민의 권리를 자격증 연령 제한처럼 임의적으로 줄이는 것은 바람직하지 않다는 생각이 든다. 생각을 바꿔서 노인 선거권제한이 아닌 대한민국 국민 전체에게 1표씩 행사하도록 하도록 바꿔보는 것은 어떨까. 그리고, 이 생각의 기원은 "No taxation without representation  대표없이 과세도 없다."이다.

'국민 스스로 선출한 국회의원의 승인없이 정부가 국민에게 과세하는 것은 부당하다는 이념 자체는 13세기에 제정된 <마그나 카르타 Magna Carta〉에서 유래하는 것으로, 이후 영국법에서 오랫동안 인민의 권리 하나로 보장해 오고 있었다.' (출처 : 위키피디아)

 현재 선거권을 인정받지 못하는 18세 이하의 국민들은 정치적 의견을 제시하지 못하고 있는  반면, 경제적 의무(세금)으로부터는 자유롭지 못하다. 비록 출산장려등으로 일시적으로 기저귀 등 일부 품목에 대한 부가세가 면세(2016년 현재)되고 있으나, 대부분 이들이 사용하는 대부분의 품목에는 부가세의 형태로 과세된다. 그 결과 미성년자들과 보호자들은 직/간접형태의 세금을 부담하고 있는 반면, 정치적 견해에 대한 반영은 '1인 1표'라는 원칙에 따라 제한되고 있는 실정이다. 그리고, 국가의 여러 정책들은 현재 선거권을 가진 노령인구에게 유리한 방식으로 입안(入案)되고 있고, 이렇게 결정된 정책의 부담은 미래세대의 몫이다. (대표적으로 국민연금 등을 들 수 있다.) 이처럼 소외된 미래세대의 목소리를 현재 정책에 반영하는 방안 중 하나로 '양육권자에게 자녀 수만큼 권리를 행사'할 수 있도록 하면 어떨까. 

 18세 연령자에게도 선거권을 부여하는 논의와는 별도로 선거권을 부여받지 못한 국민들은 양육권자에게 선거권을 부여할 경우 유권자 지도는 어떻게 바뀔까? 다음은 국가통계포털의 '2015년 인구총조사' 자료 중 일부다. 그 중 전체 49,705,663명(내국인) 인구 중 19세 이하 인구는 10,077,252명으로  전체의 20.3%에 이른다. 이 중에서 19세는 선거권이 있으니, 선거권이 없는 미성년 인구를 대략 900만명으로 가정하면, 약 900만명의 유권자가 새로 생겨나게 되는 것이다. 2015년 현재 65세 이상 인구는 6,569,082명으로 13.2%다. 현재 노령층보다 더 많은 유권자들이 생겨난다면, 정치권은 이들을 도외시한 정책을 수립하지 못할 것이다. 

[표] 2015년 인구총조사 자료 가공( by 겨울호랑이) , [출처 : 통계청,국가통계포털 http://kosis.kr/statHtml/statHtml.do?orgId=101&tblId=DT_1IN1503&conn_path=I3]

 이 경우 양육권자에게 투표권을 줄 경우, 부부(夫婦)가 자녀를 양육할 때 투표권의 귀속문제가 발생하게 된다. 한국의 현실을 고려했을 때 맞벌이 가정의 경우 어머니에게 투표권을 부여하는 것이 더 맞다는 생각이 든다. 자녀의 교육 문제 등에 대해 대체적으로 어머니들이 아버지들보다 더 많은 관심을 가고 있는 것이 사실이다. 때문에 어머니들이 자녀의 권리를 더 합리적으로 지킬 수 있지 않을까 여겨진다. 이번 대통령선거에서도 이러한 사실을 확인할 수 있었다. 제19대 대통령 선거에서 안철수 후보의 지지율이 떨어지게 된 시초는 '유치원 공약'문제였다. 대부분 아버지들은 이 문제에 대해 알지 못했지만, 어머니들은 '단설'과 '병설'의 차이와 영향에 대해 날카롭게 분석했고, 이를 비판했다. 그리고, 이후 안철수 후보의 지지율은 내리막을 달리게 되었다. 어머니들이 아버지들에 비해 자녀의 교육문제에 민감하게 반응했고, 그 결과 정치적 전환점을 마련했다는 것이 '유치원 공약 문제'라 생각된다. 이러한 내용을 근거로 어머니들의 자녀 투표권 행사가 더 바람직하다고 생각한다.

 대략 900만명의 표가 새로 발생한다면, 그리고 그 표가 대부분 여성 유권자의 증가로 이어진다면 우리 사회 소외받은 계층의 목소리가 더 커질 수 있지 않을까. 이러한 실제적 권리 개선 이후 우리 사회의 인식변화가 이루어져야 하는 것은 아닌지 다시 생각해 본다. 비록, 짧은 개인의 생각이고 실제 적용되기 위해서는 넘어야할 많은 산이 있다는 것을 알면서도 현재의 선거 제도의 문제를 통해 우리가 지향해야할 미래의 모습을 그려본다.

'맞벌이 부부의 증가 등으로 남성의 가사노동 참여 필요성이 점점 커지고 있지만, 1999~2009년 10년 사이 남성의 가사노동과 자녀돌봄 시간은 각각 하루 7분 증가하는 데 그친 것으로 나타났다. 여성의 가사노동 시간은 하루 204분으로 남성의 7.8배에 달했다.' (한국일보 2015년 3월16일자 기사)

음악은 무엇으로 하는가? 현악기에 대하여

'어떤 현(絃)이든 전체를 개방하고 퉁기면 으뜸음이 울린다. 길이를 3/4로 줄여 퉁기면 으뜸음에서 네번째 높은 "파"소리가 난다. 이 줄인 길이를 다시 2/3로 줄여 퉁기면 이번에는 "파"에서 다섯번째 높은 음이 난다. 이 과정에서 현의 길이는 정확히 원래 길이의 1/2로 줄고, 소리는 처음의 으뜸음보다 정확히 한 옥타브 높은 음이 난다. - 피타고라스(Pythagoras , BC 582 ~ BC 497)- <서양의 지혜>(p33)

1. 바이올린 Violin

'바이올린은 피아노처럼 기대를 충족시키기 위해 출현한 악기가 아니라 새로운 욕구를 만들어낸 악기죠. 이 비견할 데 없는 악기는 모든 악기를 통틀어 1730년 이후로 제조 방식이 조금도 달라지지 않은 유일한 악기입니다. 1730년은 스트라디바리(Antonio Stradivari, 1644 ~ 1737)가 바이올린을 완벽의 경지로 끌어올린 해죠. '(p63)

'콘체르티노 Concertino는 솔리스트를 모아놓은 소악기군이죠. 바이올린은 코렐리를 통하여 오케스트라의 제1소프라노라는 위엄을 얻었습니다. 하지만 이 장르의 가장 위대한 대가는 베네치아의 사제이자 천재적인 작곡가 안토니오 비발디(Antonio Lucio Vivaldi, 1678 ~ 1741)죠. 

예를 들어 비발디의 대표작인 "네 대의 바이올린을 위한 협주곡"을 봅시다. 우리는 여기서 알레그로, 라르고, 다시 피날레에서 알레그로로 이어지는 양상을 볼 수 있죠... 바흐(Johann Sebastian Bach, 1685 ~ 1750)의 "네 대의 하프시코드를 위한 협주곡"은 비발디의 "네 대의 바이올린을 위한 협주곡과 형제처럼 닮았죠.'(p65)

'바흐의 "네 대의 하프시코드를 위한 협주곡은 비발디에 대한 오마주로군요... 하지만 바흐의 아다지오는 그 잔잔한 위용이라든가, 거장중의 거장에서만 나올 수 있는 심오한 성찰의 서정성이라는 면에서 비발디를 훌쩍 넘어서 있지요.'(p65)

파가니니(Niccolò Paganini, 1782 ~ 1840)

'파가니니가 바이올린의 테크닉을 환상적으로 도약시킨 건 사실이에요. 테크닉을 완전히 변화시켰죠. 완전무결한 비르투오소의 자질들을 집약해놓은 인물이 아니었나 생각합니다... 실제로 파가니니는 네번째 현을 특히 기막히게 구사하는 연주자였죠.'(p69)

2. 첼로 Cello

'성악의 테크닉으로 말하면 첼로는 베이스, 상당히 높이 올라가는 베이스죠. 첼로야말로 가장 사람의 목소리와 비숫한 악기라면서요. 나는 무엇보다도 첼로의 피치카토 Pizzicato 주법이 흥미로운 소리를 낸다고 생각해요... 레오 들리브(Clément Philibert Léo Delibes, 1836 ~ 1891)의 발레 모음곡 <실비아>에서의 피치카토 생각 안 나요? 피치카토란 현악기를 활로 켜지 않고 손가락으로 현을 뜯는 주법이죠.

3. 콘트라베이스 Contrabass

'콘트라베이스의 쓰임새는 보통 첼로보다 한 옥타브 낮은 음으로 베이스를 강화해주는 데 있죠. 하지만 베르디와 그 이전 혹은 이후의 여러 작곡가들은 콘트라베이스 솔로도 썼습니다. 게다가 콘트라베이스의 비르투오소들도 따로 있었죠... 그 중에서 가장 유명한 사람이 지휘자 세르게이 쿠세비츠키(Sergey Koussevitzky, 1874 ~ 1951)죠.

<아레오파기티카> : 무관의 제왕(第四府)

아레오파기티카 - 언론 자유의 경전, 존 밀턴 <아레오파기티카>의 완역, 주석, 연구서
존 밀턴 지음, 박상익 옮김 / 소나무 / 1999년 2월

 "나의 양심에 따라, 자유롭게 알고 말하고 주장할 자유를, 다른 어떤 자유보다도 그러한 자유를 나에게 주십시오."

<아레오파기티카 Areopagitica>는 존 밀턴(John Milton, 1608 ~ 1674)가 저술한 언론 자유의 경전으로 평가 받고 있는 책이다. 이 책이 가지는 의의를 번역자는 다음과 같이 설명한다.

'밀턴의 <아레오파기티카>는 로크(John Locke, 1632 ~ 1704)의 관용론(A Letter Concerning Toleration, 1689)보다 거의 반세기 앞서 자유주의의 핵심 원리 및 자유주의의 철학적 기반인 개인주의(individualism)의 본질을 분명히 했다는 점에서 역사적 의의를 갖는다.'(p9)

<아레오파기티카>에서는 17세기 초반 로마 가톨릭에 의한 사상 검열을 비판하면서 출판의 자유를 강조하고 있다. 밀턴이 살았던 17세기는 갈릴레오가 종교 재판을 받고, 브루노(Giordano Bruno, 1548 ~ 1600)가 화형을 당하는 등 신학(神學)과 과학(科學) 사이의 갈등이 고조된 시기였다. 그런 점에서 당대의 지식인들에게 출판의 자유는 우리에게 '언론의 자유'만큼이나 소중한 덕목이었을 것이다. 밀턴은 출판, 언론의 자유를 어떤 내용으로 주장하였을까. 본문을 통해 살펴보자.

1. 세상의 선(善)과 악(惡)은 나눌 수 없다

 밀턴에 따르면 세상은 '선'과 '악'으로 명확히 구분될 수 없고, 불명확한 상태에서 출발하게 된다. 세상은 불순에서 순수로 나가는 과정에 있기 때문에, 악을 알기 위해서라도 이를 제거하지 않고 관찰하는 것이 필요하다.

 '우리가 이 세상에서 알고 있는 선(善)과 악(惡)은 거의 나눌 수 없을 만큼 함께 자라고 있으며, 선의 지식은 악의 지식과 너무나도 뒤얽혀 있고, 구별할 수 없을 만큼 비슷비슷해서, 프시케(Psyche)가 부단한 수고로써 분류하지 않으면 안되었던 저 뒤섞인 씨앗들도 이보다 더 혼란스럽게 섞이지는 않았을 것입니다. [514]'(p52)

'확실히 우리는 세상에 순수한 마음으로 태어나기보다는 불순한 마음으로 태어납니다. 우리를 정화하는 것은 시련이며, 무릇 시련은 반대되는 것에 의해 이루어집니다. [515](p53) ... 그러므로 이 세상에서는 악덕에 관한 지식과 관찰이 사람의 미덕을 이루는데 반드시 필요하며, 오류를 자세히 조사하는 것이 진리를 확립하는데 꼭 필요합니다.[516]'(p55)

2. 검열(檢閱)의 한계 그리고 폐해

 선과 악을 판단하는 검열관들 역시 한계를 가진 인간이기 때문에, 검열을 통해 사상을 통제하고 이상사회(理想社會)를 만들 수 없게 된다. 통제된 사회에서는 가식적인 표현만이 존재하게 된다. 밀턴은 본문에서 이탈리아의 예를 들면서 갈릴레오의 종교재판이야기를 통해 검열상태의 문제점을 지적하고 있다.

'만일 학자가 책에서 무엇인가를 처음으로 받아들이는 사람이라면, 그리고 악덕과 오류를 퍼뜨리는 사람이라면, 우리는 검열관 자신들을 어떻게 신뢰할 수 있겠습니까? 검열관에게 무오류(無誤謬)와 절대 청렴의 탁월한 미덕이 있다고 우리가 간주하거나, 그들 자신이 우리 나라의 다른 모든 사람들 이상으로 그와 같은 미덕을 갖추지 않는다면 말입니다. [520]'(p60)

 '현실을 떠나 실현 불가능한 아틀란티스나 유토피아 같은 국가로 도피하는 것으로는 우리의 상태를 개선할 수 없습니다... 플라톤이 말한 서적의 검열도 이것을 할 수 없습니다. 서적 검열은 불가피하게 수많은 다른 종류의 검열(檢閱)을 수반하게 되며, 그것은 우리 모두를 우스꽝스럽고 피곤하게 만들면서도 결국 좌절만 시킬 뿐입니다.' [526]' (p65)

'그들은 그들의 학문이 빠져 있는 굴욕적인 상태를 비통해 했습니다. [538] 이탈리아인들의 위대한 재능을 질식시킨 것은 바로 이것이었습니다. 최근 수년간 그곳에서는 아첨과 과장된 표현 이외에는 아무것도 쓰여지지 않았습니다.'(p80)

3. 삭제와 금지

검열과 삭제, 그리고 금지는 부작용을 낳는 제한적인 조치에 불과하기 때문에 궁극적인 해결방안이 되지 못한다. 그보다는 선행(언론의 자유보장)에 더 힘쓰는 것이 신(God)의 뜻에 부합하는 길이다.

'사람을 죽이는 자는 신의 형상인 이성적 창조물을 죽이는 것입니다. 그러나 좋은 책을 파괴하는 자는 이성(理性) 그 자체를 죽이는 것이며, 말하자면 눈에 보이는 신의 형상을 죽이는 것입니다. [492] '(p28)

'선과 악 어느 쪽인지 분명치 않지만, 양자에게 똑같이 유용하게 작용하는 사물을 금지하는 법률은 하찮은 것임에 틀림없다는 것을 깨달아야 합니다. 그리고 만일 내가 선택을 해야 한다면 악행을 무리하게 방지하는 것보다는 미미할지라도 선행을 하도록 하는데 몇 곱절 더 우선권이 부여되어야 한다고 생각합니다. [528]'(p67)

4. 언론 자유의 보장

 결국 검열관이 정당하게 검열할 가능성도 낮고, 검열과 삭제, 금지의 효과에 미비하다면 인간 스스로 판단할 수 있게끔 자유를 보장하는 것이 이성의 뜻, 신의 뜻에 부합하는 것이다. 비록 논쟁과 문제가 많이 발생하겠지만, 이러한 문제는 관용(寬容 tolerance)의 자세로 해결할 수 있다.

'절제(節制)란 얼마나 큰 미덕입니까, 그리고 그것은 사람의 삶에 있어서 얼마나 중요한 것입니까! 그러나 신께서는 특정한 율법이나 규제 없이, 성인들에게 전적으로 그 처분을 맡기셨습니다 [513]... 그러므로 신은 인간을 어린아이 같은 규제 속에 항상 잡아 두지 않으시고, 스스로 선택할 수 있도록 이성의 은사를 부여하셨습니다. [514]'(p51)

'[548] 사려 깊고 학식과 양식이 있는 한 사람이 자신의 견해와 논거를 위험스럽게 이 집에서 저 집으로 은밀하게 전파하는 것보다는, 그것을 공공연하게 글로 써서 세상에 공포하고, 세상 사람들이 지금 생각하고 있는 것이 건전치 못하다는 것을 드러내 보이는 것 이상으로 공명정대한 일이 무엇이겠습니까? [548] ' (p90)

'[562] 진리와 거짓으로 하여금 서로 맞붙어 싸우게 하십시오. 자유롭고 공개적인 경쟁에서 진리가 패배하는 일은 결단코 없습니다. 진리의 논박이야말로 최선의 억압이며 가장 확실한 억압입니다.'(p108)

'[554] 배우려는 욕구가 클수록 필연적으로 논쟁도 많은 법입니다. 많은 저작이 나올수록 의견도 많습니다... 얼마간의 관대한 사려와 분별, 서로에 대한 얼마간의 관용, 그리고 얼마간의 사랑만으로도 이 모든 노력을 한데 모아 진리를 향한 하나의 총체적이고도 형제다운 탐구로 통합시킬 수 있습니다.' (p99)

 불필요한 검열과 규제 대신 자유롭게 내버려두자는 밀턴의 주장에서 우리는 후대의 애덤 스미스(Adam Smith 1723 ~ 1790)가 주장한 'laissez faire'의 원형을 발견하게 된다. 흙탕물을 휘젓지 말고 내버려두면 무거운 돌들은 가라앉고 맑은 물은 위로 떠오르는 것처럼, 자유롭게 두면 모든 것이 해결된다는 것이 밀턴이 주장한 언론의 자유, 출판의 자유라 생각된다. 이러한 밀턴의 주장대로 이후 언론의 자유는 법적으로 보장되었다.

 그렇다면, 밀턴의 주장대로 헌법 제21조 1항에 따라 모든 국민은 언론, 출판의 자유와 집회, 결사의 자유를 가지는 21세기 대한민국을 살아가는 우리는 과연 선(善)한 세상에서 살고 있는가. 이에 대해 동의하는 이들은 많지 않을 것이다. 17세기에는 약자였던 언론이 21세기에는 하나의 권력으로 군림하고 있는 시대를 우리는 살고 있다. 대표적으로 제19대 대통령 선거를 며칠 앞두고 발생한 SBS의 '세월호 관련' 오보(誤報)는 이러한 우리의 현실을 잘 비춰준다는 생각이 든다.

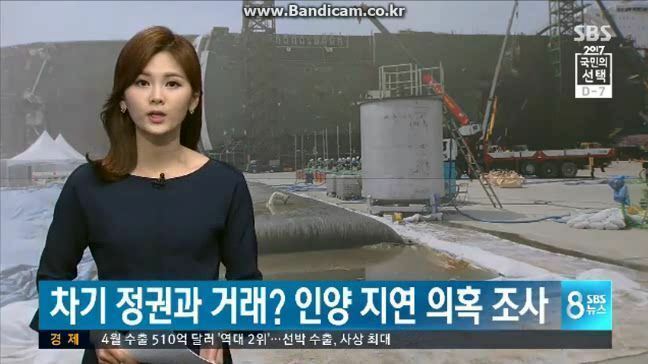
[사진] SBS 방송 오보(출처 : SBS 뉴스)

 사실 이러한 한국언론의 문제는 이명박정부 이후 10년간의 문제만은 아니다. 일제 강점기였던 1940년대 이후 우리 사회에서는 끊임없이 언론의 문제는 제기되어왔다. 1994년에 발표되었던 그룹 015B의 노래 가사에서도 우리는 언론에 대한 우리사회의 불신을 확인할 수 있다. 

드라마를 보면 언제나 상류사회뿐이고 

CF를 보면 항상 행복한 사람들 강한자에겐 무릎 굽히고 

약한자에겐 고개를 세우고 그걸 공정하다고 하지

어제는 악인을 만들고 오늘은 영웅이라하고 

아무런 생각도없이 잘도 얘기들을 하지 모든것을 비판해버리곤 

그걸 자유라 부르지 우- 우- 녹슬어진 펜을 놓고서 

우- 우- 이젠 모든말에 책임을 져 방향잃고 헤매는 가엾은 무관의 제왕 

약속을 어긴 무책임뒤엔 차가운 비웃음 뿐 

- 015B <第四府> -

 언론의 자유를 주장하는 <아레오파기티카> 속에 나타난 연구자의 모습 속에서 우리 언론인들이 나가야할 길을 발견하게 된다. 그리고 이는 시대와 관계없는 언론의 이상적인 모습이고,  변치않을 지향점이라고 생각된다. 

'한 인간이 세상을 향해 글을 쓸 때 그는 자신의 이성과 사려를 총동원합니다. 그는 탐구하고 사색하며 근면하게 노력합니다. 그는 자신의 현명한 동료들에게 자문을 구합니다. 이러한 일들을 다 거친 후에야 비로소 그는 자신이 쓴 것을 발표합니다. [532]' (p73)

 '[550] 우리는 우리의 빛을 자랑합니다. 그러나 지혜롭게 태양을 바라보지 않으면 태양은 우리를 후려쳐서 어둠으로 밀어 넣습니다... 우리가 획득한 빛은 응시하기 위해 주어진 것이 아닙니다. 그 빛에 의해 우리의 지식으로부터 저만큼 멀리 떨어진 것들을 계속 발견해내기 위해 우리에게 주어진 것입니다.' (p93)

 오랜 기간동안 달라지지 않은 언론의 문제점에 우리는 절망해 왔다. 그렇지만, 지난 6개월의 시간동안 우리는 새로운 경험을 했기에, 이제는 바꿀 수 있다는 희망을 꿈꿀 수 있다는 생각이 든다.

[사진] 촛불집회 (출처 : 불교방송)

 과거에는 핍박받던 위치에서 이제는 거대권력이 되버린 언론의 변화된 모습을 보면서 <아레오파기티카>에서 주장하는 언론 자유(自由)의 의미를 발견하는 것은 쉽지만은 않다. 그렇지만, 이제는 SNS 등의 발달로 인해 매스미디어보다는 1인 언론의 중요성이 더 커진 요즘, 진실(眞實)은 주어지는 것이 아니라 우리 스스로가 언론인(言論人)의 위치에서 판단해야 하는 상황이 되었다. 이러한 상황에서 가짜 뉴스에 현혹되지 않고 진실을 바라보는 것. 이것이 밀턴이 <아레오파기티카>에서 말하고 싶은 바는 아닐까. 언론의 자유를 통해서 우리 사회가 얼마나 밝아질 수 있는가를 묘사한 밀턴의 말을 옮기며 이번 리뷰를 갈무리한다.    

'[558] 내 마음속에는 한 고상하고 강한 국민이 잠에서 깨어난 뒤의 투사처럼 떨쳐 일어나, 천하 무적의 머리털을 흔드는 광경이 보입니다. 나는 이 국민이 마치 독수리처럼 깃털을 갈고 강인한 젊음을 되찾는 모습을, 그리고 정오의 햇살에 현란한 두 눈을 불붙여, 오랫동안 혹사한 눈을 하늘의 광휘의 원천으로 씻어내고 정화하는 광경을 봅니다.'(p103)

음악은 무엇으로 하는가? 합창에 대하여

플라톤의 <티마이오스> 음악(mousike)과 조화(harmonia)

'또한 청각(듣기)과 관련해서 시가(詩歌, mousike)의 소리에 유용한 모든 것도 조화(harmonia)를 위해 주어졌기 때문이고요. 한데, 우리 안에 있는 혼의 회전들과 동류의 운동(phora)들을 갖는 이 조화는... 우리 안에 생겨난 혼의 조화롭지 못한 회전에 대항하여 혼이 질서를 찾고 자신과 화합토록 하기 위한 원군으로서 '무사 여신들'한테서 주어졌습니다. 그리고 리듬(rhythmos) 또한 우리 대부분에 있어서 찾아볼 수 있는 적도에 어긋나고(ametron) 우아함(charis)이 부족한 상태(hexis) 때문에 같은 목적으로 같은 신들에 의해 보조자로서 우리에게 주어진 것입니다.'(47c ~ 47e)

'보세요, 매사가 그렇지만 음악에서도 조화 Harmonia는 공감을 전제로 한답니다.'(p50)

대위법(Contrepoint)의 탄생

'12세기에 탄생한 대위법은 주어진 노래에 하나 혹은 여러 멜로디를 중첩시켜 함께 나아가게 하는 기법이죠. 대위법을 도입하면 한 음표를 다른 음표와 비교해서 파악해야 하는데, 당시에는 음표를 점으로 표시했어요. 그래서 '점 대 점 Punctum contra Punctrum' 이라는 관계에서 '대위법' 이라는 용어가 나왔죠. 대위법을 사용하는 진정한 다성음악이 프랑스에서, 그러니까 12세기말 파리에서 탄생했다는 사실은 잘 알려져 있지 않은 것 같습니다. 파리 악파에 첫 영광을 안겨준 레오니우스 레오냉, 페로탱, 필립 드 비트리의 작품에서 훌륭한 예들을 볼 수 있지요.'(p51)

대위법이 일종의 점과 점의 대응이라는 관점에서 본다면, 대위법을 회화적으로도 해석할 수도 있을 것이라는 생각이 든다. 칸딘스키(W. Kandinsky)의  <점點, 선線, 면面>을 찾아보자.

'점 자체는 하나의 복잡한 통일체(그 크기 + 그 형태)이기 때문에, 점들이 점점 그 수를 더해 갈 경우 폭풍과도 같은 어떤 울림이 화면 위에 어떻게 전개되어 가는가를 쉽게 상상해 볼 수 있겠다. - 이 점들이 일치하는 경우에서도, 그리고 계속되는 과정에서 그 크기와 형태가 서로 다르고, 더욱이 크기와 형태의 차이가 점점 증가하는 점들이 화면 위에서 그려지는 경우, 이 폭풍의 전개가 어떻게 퍼져 나갈 것인가도 상상해 볼 수 있다.(p32)... 이때 점은 그것이 지닌 기하학적인 본질의 원천적인 상태로 환원되어 있다. 곧 이것은 기하학적인 무한대 속에서 그 나름대로 규칙적인 여러 가지 상이한 모습으로 부유하고 있는 기하학적인 점들의 복합체(Komplexe)이다.'(p33)

'화음'의 등장

'데 프레의 작품에서 음악은 "화음 和音" 개념에까지 다가갑니다. 이 위대한 음악가는 음악의 모든 수단을 이해하고 있었던 것 같아요. 하지만 그는 아직도 16세기 음악의 특징이 될 이 풍부한 세련미에까지 이르진 못했죠. 데 프레의 합창곡에서 목소리들은 참으로 유유히 노래합니다. 곡조가 성부들 사이를 순환하는, 아주 투명하고 경쾌하고 순수한 음악이지요.'(p53)

독일 음악과 카논 Canon

'독일 음악은 16세기에 루터의 종교 개혁과 함께 탄생했다 해도 과언이 아니죠. 그렇긴 해도 독일인들이 특히 선호해서 아주 일찍부터 갈고 닦아온 장르가 있기는 합니다. 그들은 '카논'을 좋아했지요. 카논은 합창의 여러 성부들이 같은 멜로디를 동시에 부르지 않고 어느 정도 시간차를 두고 차례차례 부름으로써 생성되는 음악적 모방 형식입니다.'(p58)

'19세기 낭만파는 드문드문 아카펠라 A Cappella, 다시 말해 무반주 합창곡을 쓰기도 했습니다. 특히 슈만과 브람스는 굉장히 아름다운 곡들을 남겼지요.'(p59)

연휴 잘 보내고 계신지요?^^: 바쁜 일정으로 일하시는 이웃분들도 계시는 것 같습니다만, 많은 분들은 연휴를 보내고 계시리라 생각됩니다. 저와 연의도 지난 어린이날 함께 시간을 보냈습니다. 미세먼지도 많아 대체로 집에서 블럭놀이를 하면서 시간을 보냈네요. 블럭놀이를 하다 에셔의 'Waterfall' 코스프레 작품을 만들어 봤습니다. 

[그림] 에셔(Esher) 'Waterfall' [출처 : http://www.mcescher.com]

[사진] 겨울호랑이와 연의의 '달팽이' - waterfall 코스프레(?)

2차원에서 시각적으로 그려진 작품을 3차원적으로 구현하기에 어려움이 있어 마지막 기둥처리가 아쉽긴 합니다만, 10분만에 블럭으로 만든 것치고는 시간 대비 작품성이 있다(?)고 생각합니다. 물론 에셔가 보면 화를 내겠지만요.^^: 이웃분들 모두 오늘 음악처럼 조화로운 하루 되시기 바랍니다.

예술에 ‘진보‘는 없습니다. ‘경향들‘이 있을 뿐이죠. 하나의 경향이 잘 전개되다가 완벽한 작품에서 정점을 찍으면 그후엔 다른 시도들이 나옵니다. 예술은 그런 식으로 생명력을 이어가고요.(p57)