-

-
학문의 진보 ㅣ 대우고전총서 35
프랜시스 베이컨 지음, 이종흡 옮김 / 아카넷 / 2002년 3월
평점 :



<학문의 진보(The Advancement of Learning)>는 1605년 프랜시스 베이컨에 의해 집필된 책이다. 베이컨은 '미답의 땅'에서 '미래'를 일구는 자신의 프로그램을 '위대한 부흥'이라고 명명하였고 이를 6부작으로 기획한다. 이 6부작 안에 <학문의 진보>, <신기관(Novun organum)>등이 포함되며, 이 중에서도 <학문의 진보>는 첫 번째 프로그램에 해당한다. <학문의 진보>는 전체 2권으로 구성되어 있다.
1권에서는 학문에 대한 오해를 바로잡고, 학문을 통한 지식의 함양이 국가와 개인의 도덕을 함양할 수 있는가에 대한 논의를 통해 '학문의 필요성'에 대해 강조한다. 이어지는 2권에서는 '지식의 분류'가 이루어진다. 지식을 '인간(人間)의 학문'과 '신(神)의 학문'으로 구분하고, 그 중에서도 인간의 학문을 역사학(歷史學), 시학(詩學), 철학(哲學)으로 구분하여 각각에 대한 분석을 시도한다. 각권의 내용을 세부적으로 살펴보면 다음과 같다.
<학문의 진보> 1권은 전체 8장으로 구성되어 있다. 1권에서 베이컨은 학문이 지금까지 불신과 불명예를 받아왔다고 주장하면서, 구체적으로 성직자들의 광신과 질시(2장), 정치가들의 가혹함과 무례함(3장), 학자들의 오류와 불완전함(4장)등을 '학문의 질병'으로 설명한다. 뒤를 이어 5장에서는 '학문의 질병을 야기하는 기질'을 논한다. 6장에서는 '신적 학문'의 원형을, 7장에서는 '인간적 학문'의 원형을 설명하면서, 1권의 마지막 8장에서는 학문을 통한 개인과 사회의 도덕성 배양을 다룬다. 결국, <학문의 진보>1권은 학문이 지금까지 받아온 오해에도 불구하고, 인간의 도덕성 함양을 위해서 필요하다는 내용으로 요약될 수 있겠다. 이러한 베이컨의 견해를 <학문의 진보>에 나오는 인용구를 통해 정리해보면 다음과 같다.
'학문의 성실한 연마는 매너를 부드럽고 인간다운 것으로 만든다. - 오비디우스, <흑해에서 온 편지(Epistulae ex Ponto) 2.9.47.> 中 - (p125)
'존재하는 모든 사물의 원인을 아는 자는 얼마나 행복한가.
그는 모든 공포, 냉혹한 운명을 발 아래 두고, 지하에서 굉음을 내며 흐르는 탐욕스런 아케론 강물 위에, 평화롭게 서 있노라. - 베르길리우스, <지오르직스(Georgics)2.490> 中 - (p127)
<학문의 진보>2권에서는 베이컨의 분류한 학문에 대해 개별적으로 분석을 한다. 전체 25장의 내용을 여기에서 다 요약하기는 어려움이 있어 책 뒷부분에 수록된 '해제'의 이미지를 통해 세부 내용을 대신한다.
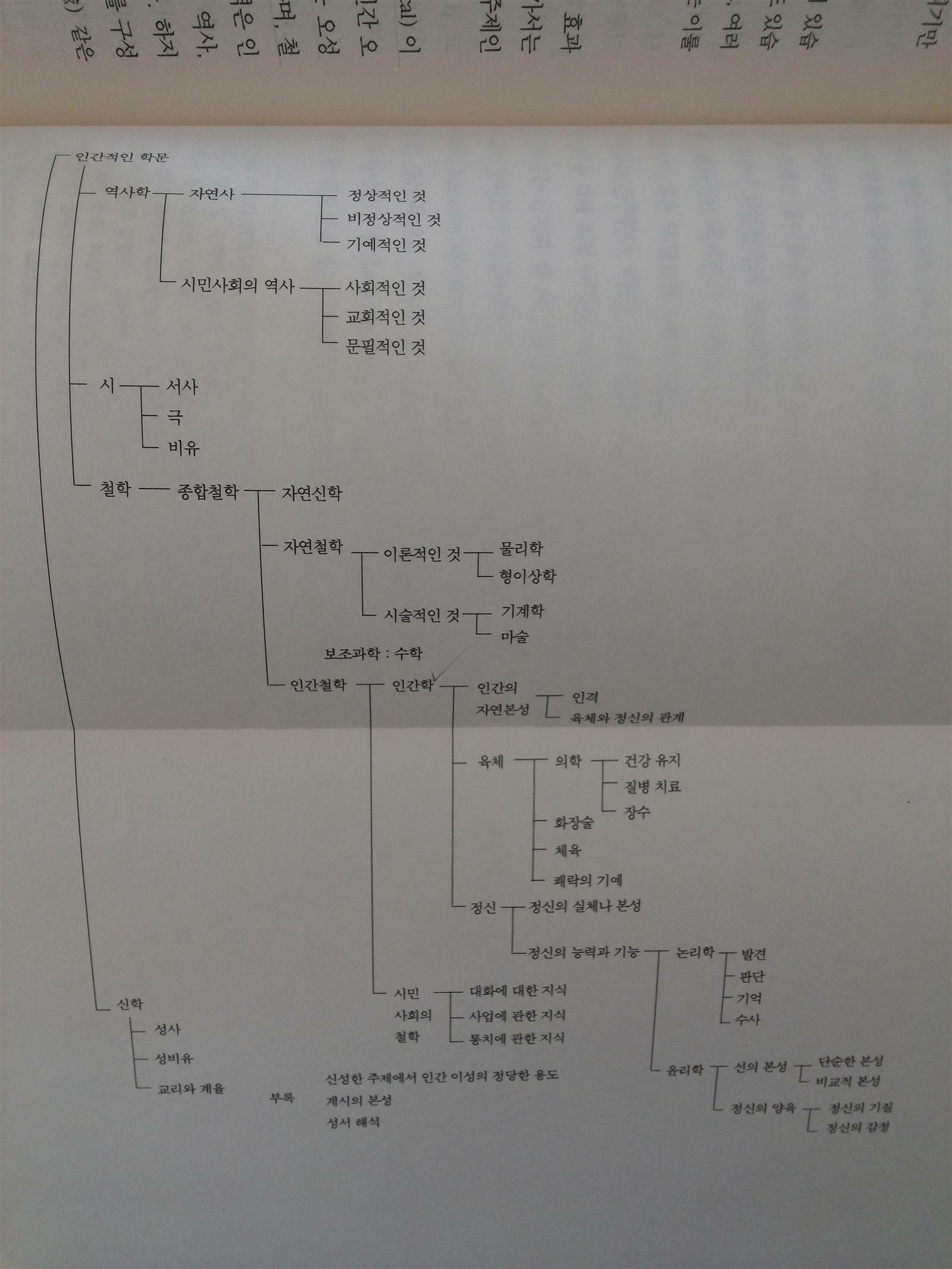
[그림] 베이컨의 지식 분류 체계
<학문의 진보>2권에서는 [그림]과 같이 정리된 베이컨의 지식 분류 체계의 내용을 베이컨의 주장과 이에 해당하는 근거(성경, 고대 그리스/로마 문학 작품 등)를 제시하고 있다. 여기에서 프랜시스 베이컨이 인식하고 있는 학문체계와 개랸적인 내용에 대한 밑그림이 제시되는데, 이를 통해 베이컨이 생각했던 '위대한 부흥'의 구조를 어느 정도 이해할 수 있다.
베이컨의 책은 읽기 어려운 점이 있는데 이는 그의 문체(文體)에 기인하는 것 같다. <학문의 진보> - 해제: 왜 다시 프랜시스 베이컨인가? - 에서는 그의 문체의 특성을 다음과 같이 정리한다.
'아포리즘(Aphorism)'은 <신기관(Novun organum)>에서 사용된 지배적인 문체이다. 지식의 '핵심'만을 명료하게 전하되, 그 '핵심'을 논리적으로 체계화하지는 않는 문체이다. 실제로 베이컨은 그 문체에 의해 지식의 산개(散開)를 시도하면서, 이는 독자들이 현재의 지식에 만족하지 않고 지식의 진보에 힘쓰도록 하기 위한 것이라고 주장한다.(p324)
<학문의 진보>를 읽다보면 마치, 베이컨이 신제품을 만들어 놓고 독자들 앞에서 이 제품에 대해 설명과 동시에 분해한 뒤 독자들에게 다시 조립할 것을 요구하는 느낌을 준다. 내가 이해력이 부족해서인지는 몰라도 베이컨의 서술만 따라가다보면 내용이 머리에 잘 정리되지 않는 어려움이 있었다. 좀 더 깊이 있는 독서를 위해서는 다독(多讀)이 필요한 책이라 생각된다.
위의 내용을 종합적으로 정리하면, <학문의 진보>는 공부의 목적과 학문(學問)을 분류/제시한 책이라 하겠다. 이를 통해 우리가 왜 배워야 하는지, 무엇을 공부해야하는 지를 알 수 있다는 면에서 평생공부의 밑그림을 그리는데 참고가 될 수 있는 책이라 생각된다. 개인적인 의견이지만 <학문의 진보>와 동양 고전인 <대학(大學)>을 비교해서 읽는 것도 의미가 있을 것 같다. 동양과 서양의 학문의 목적에 대해 논의한 두 책이기에 같은 주제를 다루지만, 입장은 조금 다르다.
<학문의 진보>의 결론이 '아는 것이 힘이다.(Knowledge is power)'라는 문장으로 나간다면 , <대학>에서는 '大學之道 在明明德'으로 학문의 목적이 요약되기에 두 문명권의 사상 비교와 이후 사상의 발전을 생각해보면 보다 재미있을 것 같다.
PS. <학문의 진보>(1605)와 <신기관>(1620) 사이 기간동안 베이컨은 정치적으로 크게 성공한 인물이었다. 1604년 국왕의 법률고문, 1607년 법무차관, 1614년 법무장관을 역임하는 등 그는 성공한 법률가였다. 그러던 중 1621년 5월 프랜시스 베이컨은 뇌물수수죄로 체포,잠시 런던탑에 투옥되었다. 이후 그의 인생은 급격한 몰락의 길을 걷게 된다. <학문의 진보>에는 마치 그런 자신의 모습을 변명하는 듯한 글이 보여 마지막으로 옮겨본다.

[그림] 프랜시스 베이컨(출처 : 위키피디아)
<재판에서 사람의 낯을 보아주는 것이 좋지 못하고, 한 조각 떡으로 인하여 범법하는 것도 그러하니라>. 이 아포리즘에서는, 인정에 끌리는 재판관보다는 차라리 뇌물받는 재판관이 낫다는 점이 지적된다. 부패한 재판관이 줏대 없는 재판관보다는 쉽게 죄를 범하지 않는다는 것이다.(p414)